Log‑Periodic Dipole Array Calculator
Serge Stroobandt, ON4AA
Michael McCue, W7YZT
Copyright 2014–2020, licensed under Creative Commons BY-NC-SA
- Home
- LPDA Calculator
Overview

HF wire antenna rendering of a log‑periodic dipole array.
Drawing by: Michael McCue, W7YZT ©2017–2018

Detail of the end‑fed feed of a VHF log‑periodic dipole array. The feed coax is routed through the inside of the right boom. Only the center conductor of the coaxial cable is connected to the left boom by means of a rivet. The dipole elements are threaded on the outside. Polymer standoff insulators between the parallel booms are also visible. Use my parallel square transmission line calculator to determine the correct boom separation distance, given \(Z_\text{c,feed}\).
Free-space directivity

- The free-space directivity of a log-periodic dipole array (LPDA) is a function of its taper \(\tau\) and its chosen spacing \(\sigma\).1–5 Decreasing \(\sigma\) will decrease the boom length \(L\). Decreasing \(\tau\) will decrease both the boom length \(L\) and the number of elements \(N\). Due to space and resource constraints, amateur radio log-periodic antennas are often limited to values of \(\tau\) between 0.88 and 0.95, with values of \(\sigma\) between 0.03 and 0.06.6
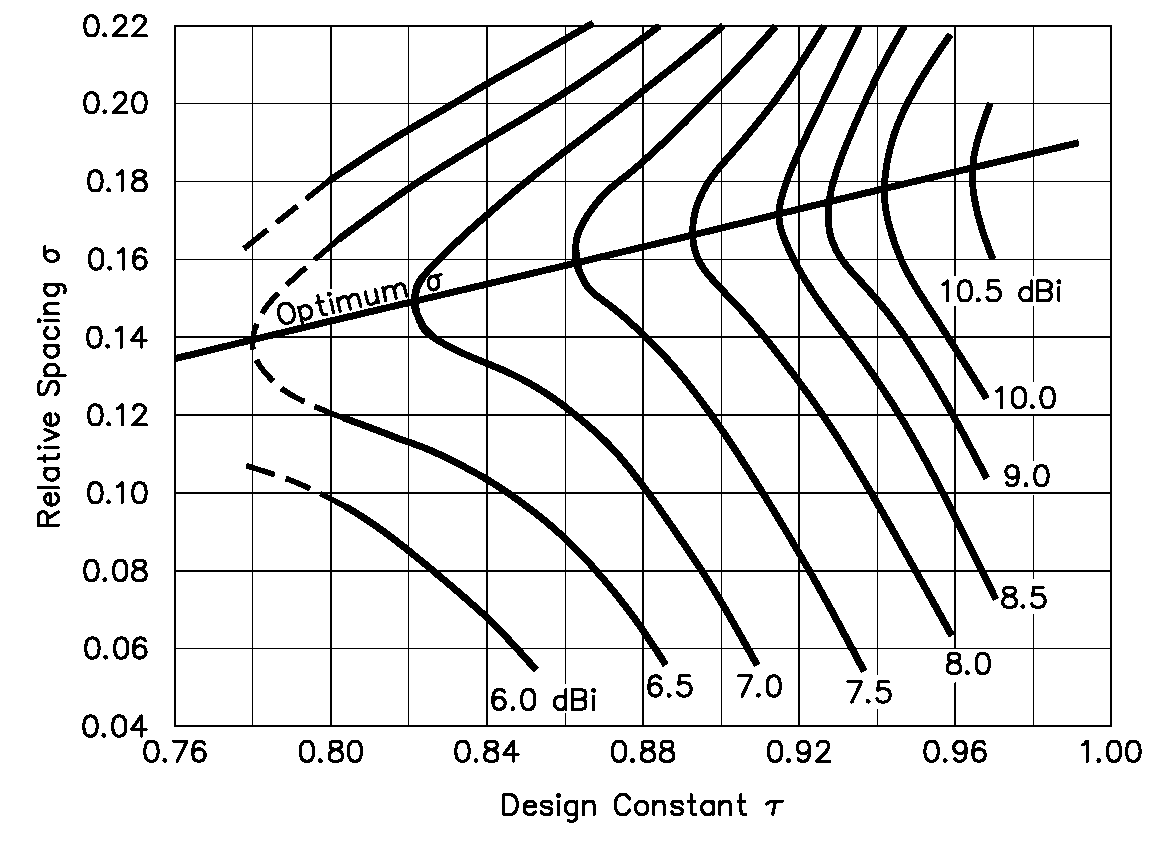
Free-space directivity of a log-periodic dipole array as a function of its taper \(\tau\) and spacing \(\sigma\) for \(Z_\text{c,feed}=100\,\Omega\) and \(\frac{\ell_i}{⌀_N}=125\). Source: Hutira et al.7
Input
Input guidelines:
- * Choose a slightly broader frequency range to compensate for construction inaccuracies.
- † The characteristic input impedance \(Z_\text{c,in}\) of an LPDA is to a large extent determined by the dimensions of the shortest element. In a true LPDA, element diameters should scale proportionally to element length. However, keeping element diameters the same throughout an LPDA turns out to be pretty forgiving in many cases.
- ‡ Every so often, HF LPDAs are designed with a characteristic input impedance of 200 Ω; a 4÷1 current balun transforms the impedance to 50 Ω. On VHF and higher frequencies, LPDAs are normally designed for a direct connection to a 50 or 75 Ω characteristic input impedance.
Resulting design
Design notes:
- * The width of any antenna boom is included within the length of each dipole element, as one would do for any ordinary dipole or Yagi-Uda antenna.
- † The terminating stub \(Z_\text{term}\) is only required when the characteristic impedance of the feeder \(Z_\text{c,feed}\) is low. This is typical of VHF and UHF arrays.6,8 A terminating stub improves the front‑to‑back ratio at «weak spots» in the frequency domain.6,7 Moreover, a stub prevents static charge build‑up on the connecting transmission line.6 Hutira7 prescribes a stub length of λ1/4; i.e. double the length given by Cebik6 and this calculator. Model or experiment with different stub lengths to select the most useful radiation pattern.6
- ‡ The feeder connecting the elements is a parallel conductor transmission line. The separation distance between the parallel conductors determines the characteristic impedance \(Z_\text{c,feed}\) of this transmission line, which is different from the input impedance \(Z_\text{c,in}\) of the antenna. The separation distance can be calculated using either my parallel square or circular conductor transmission line calculator.
Copy & paste
Formulas
This LPDA calculator is mainly based on the design procedure as described by L. B. Cebik, W4RNL (SK) in the 21st edition of The ARRL Antenna Handbook.6 The calculator was successfully tested against the examples listed in this reference. Unlike the book, this calculator employs the velocity of light \(c\) at full precision, resulting in slightly shorter, but more precise lengths. Furthermore, the formula for computing the boom length \(L\) has been improved by not including the distance to the virtual apex \(2\alpha\) of the antenna.
\[B = \frac{f_\text{n}}{f_1}\]
\[\tau\equiv\frac{\ell_i}{\ell_{i-1}} \qquad 0.8 \leq \tau \leq 0.98\]
\[\sigma\equiv\frac{d_{1,2}}{\lambda_1} \qquad \sigma_\text{opt} = 0.243\:\tau - 0.051 \qquad 0.03 \leq \sigma \leq \sigma_\text{opt}\]
\[\cot\alpha = \frac{4\,\sigma}{1 - \tau}\]
\[B_\text{ar} = 1.1 + 7.7\,\left(1 - \tau\right)^2\cot\alpha\]
\[B_\text{S} = B\cdot B_\text{ar}\]
\[N = 1+\frac{\ln B_\text{S}}{\ln\frac{1}{\tau}} \qquad \begin{cases} \{N\} \gt 0.3 \rightarrow \lfloor N\rceil = \lceil N\rceil\\ \{N\} \le 0.3 \rightarrow \lfloor N\rceil = \lfloor N\rfloor \end{cases}\]
\[c \equiv 299\,792\,458\,\frac{m}{s}\]
\[\ell_1 = \frac{\lambda_1}{2}=\frac{c}{2\,f_1} \qquad \ell_i = \tau \cdot \ell_{i-1} \qquad \ell_{tot} = \sum\limits_{i=1}^{n}\ell_i\]
\[d_{i,i+1} = \frac{\ell_i-\ell_{i-1}}{2}\,\cot\alpha \qquad L = \sum\limits_{i=1}^{n-1} d_{i,i+1}\]
\[\ell_{Z_\text{term}} = \frac{\lambda_1}{8}\]
\[Z_{\text{c,}N} = 120 \left[ \ln \left( \frac{\ell_N}{⌀_N} \right) - 2.25 \right] \qquad \sigma'\equiv\frac{\sigma}{\sqrt{\tau}}\]
\[Z_\text{c,feed} = \frac{Z_\text{c,in}^2}{8\,\sigma'Z_{\text{c,}N}} + Z_\text{c,in} \sqrt{\left( \frac{Z_\text{c,in}}{8\,\sigma'Z_{\text{c,}N}} \right)^2 + 1}\]
Brython source code
Here is the Brython code of this calculator. Brython code is not intended for running stand alone, even though it looks almost identical to Python 3. Brython code runs on the client side in the browser, where it is transcoded to secure Javascript.
References

This work is licensed under a Creative Commons Attribution‑NonCommercial‑ShareAlike 4.0 International License.
Other licensing available on request.

Unless otherwise stated, all originally authored software on this site is licensed under the terms of GNU GPL version 3.
This static web site has no backend database.
Hence, no personal data is collected and GDPR compliance is met.
Moreover, this domain does not set any first party cookies.
All Google ads shown on this web site are, irrespective of your location,
restricted in data processing to meet compliance with the CCPA and GDPR.
However, Google AdSense may set third party cookies for traffic analysis and
use JavaScript to obtain a unique set of browser data.
Your browser can be configured to block third party cookies.
Furthermore, installing an ad blocker like EFF's Privacy Badger
will block the JavaScript of ads.
Google's ad policies can be found here.
transcoded by
 .
.


